fertmidwest.blogg.se - Continuity calculus problems

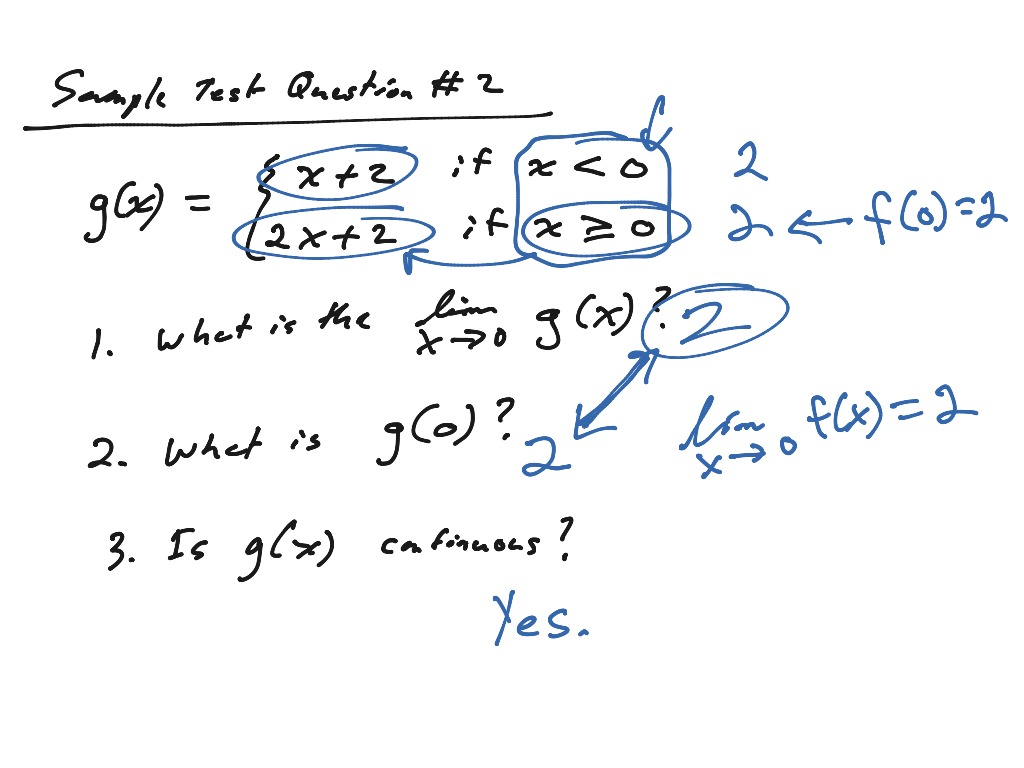
Even if a function is “normal”, like a linear function, we still consider the \(y\)-value a limit where it touches the \(x\)-value, as shown below. Now the beauty of limits is that \(x\) can get closer and closer to a number, but not actually ever get there (think asymptote from the Rational Functions section). We can write a limit where \(x\) gets closer and closer to 0 as \(\underset\)”. Again, remember that limits are always the \(y\)-value (dependent variable), not the \(x\)-value (independent variable). (Differential calculus has to do with rates at which quantities change.) I like to think of a limit as what the \(y\)-part of a graph or function approaches as \(x\) gets closer and closer to a number, either from the left-hand side (which means that \(x\)-part is increasing), or from the right-hand side (which means the \(x\)-part is decreasing).

We need to understand how limits work, since the first part of Differential Calculus uses them extensively. Also note that there’s a very good limit calculator here on the this online calculator site. Note that we discuss finding limits using L’Hopital’s Rule here. Introduction to Limits Intermediate Value Theorem (IVT) Finding Limits Algebraically Infinite Limits Continuity and One Side Limits Limits at Infinity Continuity of Functions Limits of Sequences Properties of Limits More Practice Limits with Sine and Cosine

Applications of Integration: Area and Volume.

Exponential and Logarithmic Integration.

Riemann Sums and Area by Limit Definition.

Differential Equations and Slope Fields.

Antiderivatives and Indefinite Integration, including Trig.

Derivatives and Integrals of Inverse Trig Functions.

Exponential and Logarithmic Differentiation.

Differentials, Linear Approximation, Error Propagation.

Curve Sketching, Rolle’s Theorem, Mean Value Theorem.

Implicit Differentiation and Related Rates.

Equation of the Tangent Line, Rates of Change.

Differential Calculus Quick Study Guide.

Polar Coordinates, Equations, and Graphs.

Law of Sines and Cosines, and Areas of Triangles.

Linear, Angular Speeds, Area of Sectors, Length of Arcs.

Conics: Circles, Parabolas, Ellipses, Hyperbolas.

Graphing and Finding Roots of Polynomial Functions.

Graphing Rational Functions, including Asymptotes.

Rational Functions, Equations, and Inequalities.Solving Systems using Reduced Row Echelon Form.The Matrix and Solving Systems with Matrices.Advanced Functions: Compositions, Even/Odd, Extrema.Solving Radical Equations and Inequalities.Solving Absolute Value Equations and Inequalities.Imaginary (Non-Real) and Complex Numbers.Solving Quadratics, Factoring, Completing Square.Introduction to Multiplying Polynomials.Scatter Plots, Correlation, and Regression.Algebraic Functions, including Domain and Range.

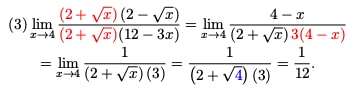
Systems of Linear Equations and Word Problems.Introduction to the Graphing Display Calculator (GDC).Direct, Inverse, Joint and Combined Variation.Coordinate System, Graphing Lines, Inequalities.Types of Numbers and Algebraic Properties.Introduction to Statistics and Probability.Powers, Exponents, Radicals, Scientific Notation.